9 基本的な展開手法

前章までは平面を対象とした幾何図法について述べてきたが、立体構造から成る船体を造り出すためには、その構成部材を平面に展開する作業が必要となる。現図作業の中において最も分かりにくいものが、この展開作業であろう。

本章においては、現図作業を理解するための準備段階として、基本的な展開手法について触れることとする。

9.1 平行線法

この方式は、展開しようとする部材の中に平行線を構成している部分を見つけ出して、それを利用する方法である。したがって、この場合は、設定した個々の平行線の間の距離が分からなければならない。

例えば図1.39のような円筒形に切込みのあるものの展開図形を求める場合、図の左側の平面図と正面図が与えられているときに、右側のような展開図を求めることになる。この左側の図をみると、平面図には円周の実長が表わされているので、この円周を適当な区分で切ってその位置に垂直線を立てれば、それぞれの垂直線は平行線となる。四角柱のようなものであれば、最初からその稜を使えばそれが平行線になるが、この例のように自分で適切な平行線を引かなければならないこともある。この補助の平行線を引けば、展開はこの平行線だけに着目して行えばよい。即ち円周の長さは、平面図から実長が読みとれるから、1直線上にそのそれぞれの区分点の位置を記し、その上に設定した平行線の長さだけを引出す。その後それぞれの点を滑らかに結ぶようにすることによって、展開図形が求められる。

この手法は、ホースパイプの展開に、そっくりそのまま使用できる即ち、ホースパイプは、正面線図や平面図に対して斜めに配置されているが、これを切直して、図1.39のような位置に見えるように方向をまわしてから、この平行線法を使うのであるまた、内構材のストリンガー等の展開に際しても、この手法で展開図形を得られることが多いはずである。

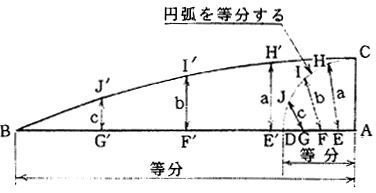
図1.39

前ページ　　　目次へ　　　次ページ